Fixed Point Theory and Applications
 Fixed Point Theory and Applications
Fixed Point Theory and Applications
Welcome to the future Book on Fixed Point Theory and Applications on the Web. I would like to ask anyone who is interested to be part of this wonderful project. The idea is very simple: Choose one of the following topics and write down something in Latex, mail it to me and I will be glad to put it here under the author's name. This way this project will not be a burden on one person.
-
-
Chapter 0. Introduction
-
-
Chapter 1. The Contraction Principle
- 1.
- Historical Notes
- 2.
- The Contraction Principle in Complete Metric Spaces
- 3.
- Applications
- 3.1
- Differential Equations
- 3.2
- Implicit Theorem
- 3.3
- Holomorphic Mappings
- 3.4
- Perron-Frobenius Theorem
- 3.5
- Fractal sets: The Cantor set
- 4.
- Menger Spaces
-
-
Chapter 2. Nonexpansive Mappings in Hilbert Spaces
- 1.
- Some Examples
- 2.
- Classical Theorems
- 2.1
- Demi-Closeness Principle
- 2.2
- Existence of Fixed Point
- 3.
- Semi-group of Nonexpansive Mappings
- 3.1
- Basic Definitions
- 3.2
- Generator
- 3.3
- Accretivity, Monotone Operators
- 3.4
- Resolvent
- 3.5
- Theorems
- 3.6
- Example:
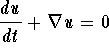
- 4.
- Commuting Families
- 5.
- Uniformly Lipschitzian Maps
- 6.
- Applications
- 6.1
- Periodic Solutions
- 6.2
- Forcing
-
-
Chapter 3. Nonexpansive Mappings in Banach Spaces
- 1.
- Classical Counter Examples
- 1.1
-
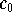 ,
, 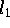
- 1.2
-
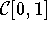
- 1.3
- Alspach's counter example
- 2.
- Uniformly Convex and Uniformly Smooth Banach Spaces
- 2.1
- Basic Definitions
- 2.2
- Examples
- 2.3
- Properties
- 2.4
- Scaling of the Unit Ball
- 3.
- Fixed Point Theorems
- 3.1
- Demi-Closeness Principle
- 3.2
- Browder-Gohde Theorem
- 3.3
- Contraction of Type-(
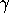 )
)
- 3.4
- Acretive Operators
- 3.5
- Asymptotic Center Technique
- 3.6
- Minimal points and Optimal Points
- 4.
- Normal Structure Property
- 4.1
- Basic Definitions and Examples
- 4.2
- Characterizations: Brodskii-Milman-Landes
- 4.3
- Some Counter Examples
- 4.4
- Spaces with Normal Structure Property
- 4.5
- Normal Structure Property in Spaces with Bases
- 5.
- Ultraproduct Techniques
- 5.1
- Basic Definitions
- 5.2
- Basic Results in Ultraproduct Language
- 5.3
- Fixed Point Theorems
- 5.3.1
- Uniformly Convex Spaces
- 5.3.2
- Lin's results and its Extensions
- 5.3.3
- Maurey's Fixed Point Theorems
- 6.
- Lattice Banach Spaces
- 6.1
- Remarks on Maurey's
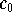 -Fixed point Theorem
-Fixed point Theorem
- 6.2
- Borwein-Sim's Fixed Point Theorem
- 7.
-
 -Fixed Point Property
-Fixed Point Property
- 7.1
- Examples and Counter Examples
- 7.2
-
 -Fixed Point Property
-Fixed Point Property
- 7.3
-
 -Normal Structure Property
-Normal Structure Property
- 7.4
- in Lattice Banach Spaces
-
-
Chapter 4. Orbit, Omega-set
- 1.
- Basic Definitions
- 2.
- Compact Orbit
- 3.
- Classical Techniques in Hilbert space
- 4.
- Periodic Points
- 5.
- Iterative Processes
- 6.
- Applications
- 6.1
- Atractors
- 6.2
- Chaos
-
-
Chapter 5. Ergodic Theorems
- 1.
- Classical Linear results
- 2.
- Baillon's Theorem
- 3.
- Extensions: Amenable Semi-Group
- 4.
- Asymptotic Behavior
- 5.
- Examples
-
-
Chapter 6. Approximation Techniques
-
-
Chapter 7. Non-classical Banach Spaces
- 1.
- Orlicz spaces
- 2.
- James' spaces
- 3.
- Tsirelson' spaces
-
-
Chapter 8. Metric Spaces
- 1.
- Basic Definitions
- 2.
- Examples
- 2.1
- Unit Ball of
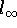
- 2.2
- Unit Ball of the Hilbert space
- 3.
- Nonexpansive Mappings in Metric Spaces
- 3.1
- Convexity Structures in Metric Spaces
- 3.2
- Normal Structure Property in Metric Spaces
- 3.3
- Kirk's analogue in Metric Spaces
- 3.4
- Holomorphic Maps on the Unit Ball of the Hilbert space
- 4.
- Hyperconvex Metric Spaces
- 4.1
- Basic Definitions
- 4.2
- Basic Properties
- 4.3
- Fixed Point Theorems
-
-
Chapter 9. Measure of Non-compactness
- 1.
- Basic Definitions
- 2.
- Examples
- 3.
- Condensing Mappings
- 4.
- Approximation
- 5.
- Applications
-
-
Chapter 10. Caristi's Fixed Point Theorem
- 1.
- Caristi's Fixed Point Theorem
- 2.
- Ekeland's Principle
- 3.
- Equivalent Theorems
- 4.
- Normal Solvability
- 5.
- Examples and Applications
-
-
Chapter 11. Bifurcation Theory
-
-
Chapter 12. Multivalued Mappings
-
-
Chapter 13. Generalized Structures
- 1.
- Definition of an Ordered Set
- 2.
- Tarski's Fixed point Theorem
- 3.
- Applications
- 3.1
- Godel's Theory
- 3.2
- Graph Theory
- 3.3
- Logic Programming
- 4.
- Generalized Metric Spaces
- 4.1
- Basic Definitions
- 4.2
- Examples
- 4.3
- Hyperconvex Generalized Metric Spaces
- 4.4
- Fixed Point Theorems in Generalized Metric Spaces
- 4.5
- Fixed Point Theorems for Families
- 4.6
- Product Spaces
- 4.7
- Applications
- 5.
- Modular Spaces
-
-
Chapter 14. Topological Fixed Point Theory
- 1.
- Finite Dimension
- 1.1
- Brower's Theorem
- 1.2
- Minimax Theorems
- 1.3
- KKM-Maps
- 1.4
- Homology and Kohomology
- 1.5
- Degree Theory
- 1.6
- Sperner's Lemma
- 1.7
- Computation Techniques
- 1.8
- Applications
- 1.8.1 Game Theory
- 1.8.2 Economics
- 1.8.3 Logic Programming
- 1.9
- Hoft Construction
- 1.10
- discrete Brower's Theorem
- 2.
- Infinite Dimension
- 2.1
- Leray-Schauder's Fixed Point Theorem
- 2.2
- Degree Theory
- 2.3
- ANR' Sets
- 2.4
- Nielson Theorems
- 2.5
- Lefschetz Fixed Point Theorems
- 2.6
- Bifurcation Theory
- 2.7
- Applications
- 3.
- Miscellanous
- 3.1
- Complementarity Problems
- 3.2
- Renorming Techniques
- 3.3
- Most Recent Fixed Point Theorems
 Fixed Point Theory and Applications
Fixed Point Theory and Applications Fixed Point Theory and Applications
Fixed Point Theory and Applications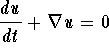
![]() ,
, ![]()
![]()
![]() )
)
![]() -Fixed point Theorem
-Fixed point Theorem
![]() -Fixed Point Property
-Fixed Point Property
![]() -Fixed Point Property
-Fixed Point Property
![]() -Normal Structure Property
-Normal Structure Property
![]()